MachineLearning(9) OREILLY(6) Python(9)

### 前回まで [前回の記事](/articles/6)にて環境構築や機械学習の基礎をまとめたので、今回からは簡単な実践を行っていきます。 <center> <a href="http://www.amazon.co.jp/gp/product/4873116988/ref=as_li_qf_sp_asin_il?ie=UTF8&camp=247&creative=1211&creativeASIN=4873116988&linkCode=as2&tag=koucs-22"><img border="0" src="http://ws-fe.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=4873116988&Format=_SL250_&ID=AsinImage&MarketPlace=JP&ServiceVersion=20070822&WS=1&tag=koucs-22" ></a><img src="http://ir-jp.amazon-adsystem.com/e/ir?t=koucs-22&l=as2&o=9&a=4873116988" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /> </center> ### 1章 Pythonではじめる機械学習 （つづき） #### 1.5 はじめての（簡単な）機械学習アプリケーション ###### __シチュエーション__ 　HTTP経由で機械学習アルゴリズムを販売している会社であるM社は、今後増加するwebリクエストに対応するためにインフラの整備が必要である。 　現在のインフラは100,000件のリクエスト/時間に対応できるものとし、クラウドにあるサーバを構築しなければならない時間を事前に予測し、余分なサーバ費用をできるだけ発生させずにwebリクエストの増加に対応したい。 ###### 1.5.2 前処理とデータ整形 　今回解析に用いるデータは2次元のデータポイントが743個で構成されています。（[データ](https://github.com/luispedro/BuildingMachineLearningSystemsWithPython/tree/master/ch01/data)） 　1つ目のベクトル（x）は時間、もう一つのベクトル（y）はアクセス数を指しており、743時間（約４週間）分のデータが格納されています。 ``` bash >>> import scipy as sp >>> data = sp.genfromtxt("./web_traffic.tsv", delimiter="\t") >>> >>> data array([[ 1.00000000e+00, 2.27200000e+03], [ 2.00000000e+00, 1.65600000e+03], [ 3.00000000e+00, 1.38600000e+03], ..., [ 7.41000000e+02, 5.39200000e+03], [ 7.42000000e+02, 5.90600000e+03], [ 7.43000000e+02, 4.88100000e+03]]) >>> >>> data.shape (743, 2) ``` 　このデータを散布図としてプロットするには、以下のコードで記述する。（[データ](https://github.com/luispedro/BuildingMachineLearningSystemsWithPython/tree/master/ch01/data)） ``` python # coding: UTF-8 import scipy as sp import matplotlib.pyplot as plt if __name__=='__main__': data = sp.genfromtxt("./web_traffic.tsv", delimiter="\t") x=data[:,0] y=data[:,1] plt.scatter(x,y) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w*7*24 for w in range(10)], ['week %i'%w for w in range(10)]) plt.autoscale(tight=True) plt.grid() plt.savefig('./images/ch1-5_plt1.png') ```  ###### 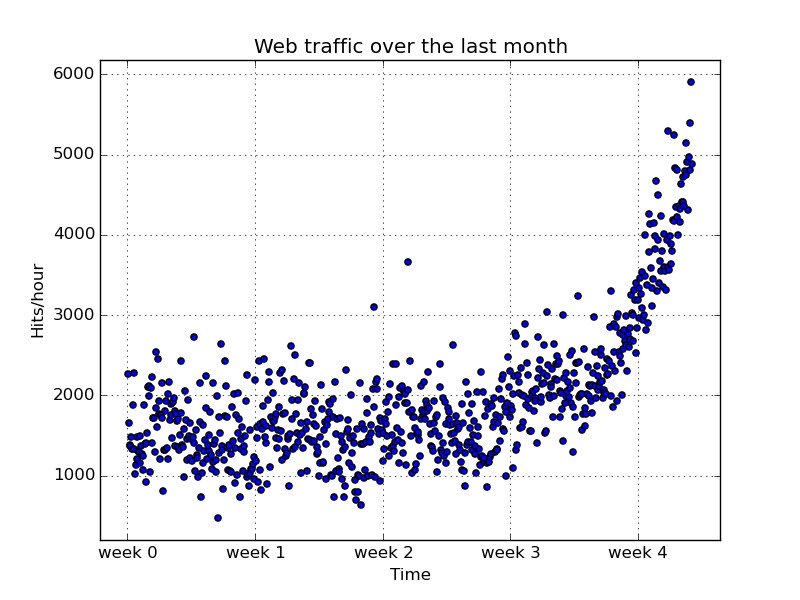単純な曲線で近似する > 扱う対象が直線で表現できる単純なモデルであると仮定する。そうすると、考えるべき問題は上記のグラフ上でどのように直線を配置したら近似誤差を最小にできるかということになります。 ここでいう近似誤差を最小にする手法とは、[SciPyのpolyfit()](http://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html)です。 __# 1次式で (x,y) 2 変数の回帰分析__ __fp1 = sp.polyfit(x, y, 1)__ > __回帰分析とは__ 変数間に一方 x が他方 y を左右ないし決定する影響があるとき、 x を 独立変数 (independent variable) 、 Y を 従属変数 (dependent variable) と言います。 この関係式を要約して直線を当てはめるのが線形回帰です。 > [参考](http://qiita.com/ynakayama/items/5732f0631c860d4b5d8b) polyfitを用いて本データを回帰分析で導いた直線で近似させてみます。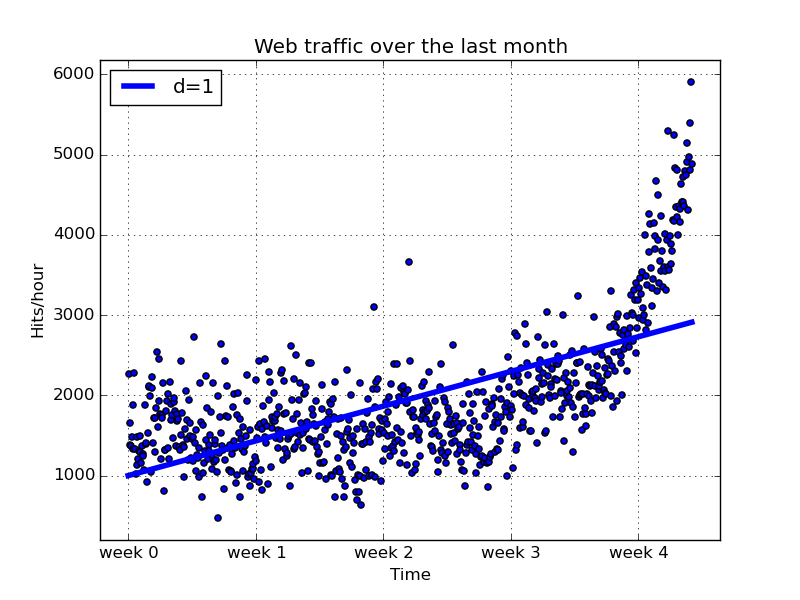 ``` python fp1, residuals, rank, sv, rcond = sp.polyfit(x, y, 1, full=True) print("Model parameters: %s" % fp1) f1 = sp.poly1d(fp1) fx = sp.linspace(0, x[-1], 1000) plt.plot(fx, f1(fx), linewidth=4) plt.legend(["d=%i" % f1.order], loc="upper left") plt.savefig("./images/ch1-5_plt2.png") ```  ・・・これは将来のアクセス予測には使えなさそうです。 ### ここまでのまとめ 　ここまで求めた回帰分析の近似直線ではまだまだアクセス予測ができるものにはなっていません。ここからさらに工夫を凝らし、より良い解析を行っていくこととなるのですが、それはまた次回の記事で。