MachineLearning(9) OREILLY(6) Python(9)

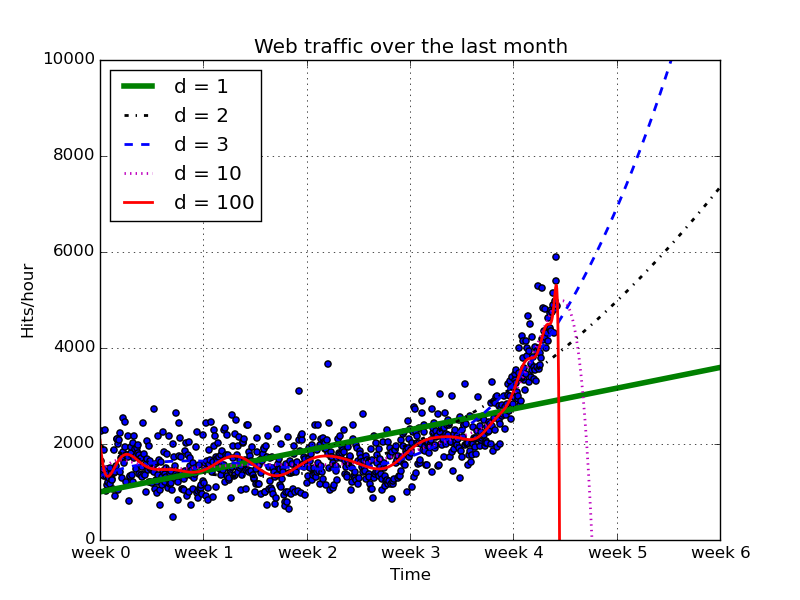
### 前回まで [前回の記事（第２回）](/articles/10)にてWebアクセス数のログデータから今後のトラフィック予測を行うという目的のため、回帰分析の近似直線を引いて分析を行っていました。 <br /><br /> ### 1.5.3 正しいモデルの選択と機械学習 　前回から引き続いて、次数が1, 2 ,3 10,100の5パターンで検証してみます、また、今までは4.5週間という、学習データがある部分しかプロットしなかったのですが、それ以降の値も検証し、学習したモデルで未来のトラフィックを予測させてみます。  　次数10と100（d=10, 100）からなるモデルは、未来を全く予想出来ていないことがわかります。訓練データに適合させすぎたことから、未来を予想することに関しては適していないことがわかります（*過学習*）。 　一方、次数の低いモデルはデータを掴み取れていないようです。（*未学習*）。 <br /><br /> #### データを違う視点から眺める 　ここでデータを改めて見てみると、3.5週目あたりからデータの形態が変わっているように見えます。ここで視点を変えて、*3.5週目以前*と*3.5週目以降*のデータを分けて検証していきます。 ``` python # 3.5週以降を別のグラフで近似させる inflection = 3.5*7*24 xa = x[:inflection] ya = y[:inflection] xb = x[inflection:] yb = y[inflection:] fa = sp.poly1d(sp.polyfit(xa, ya, 2)) fb = sp.poly1d(sp.polyfit(xb, yb, 2)) fa_error = error(fa, xa, ya) fb_error = error(fb, xb, yb) print("Error inflection=%f" % (fa_error + fb_error)) plt.clf() plt.scatter(x,y) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w*7*24 for w in range(10)], ['week %i'%w for w in range(10)]) plt.axis([0, 24*7*6, 0, 10000]) plt.grid() plt.plot(fx[:inflection], fa(fx[:inflection]), linewidth=4) plt.plot(fx[inflection:], fb(fx[inflection:]), linewidth=4) plt.legend(loc="upper left") plt.savefig("./images/ch1-5_plt5.png") ```  　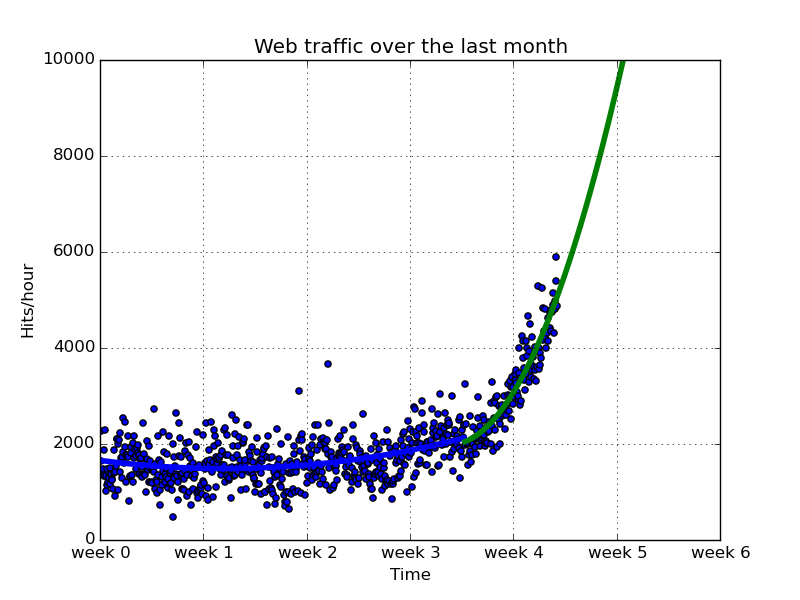たしかに、3.5週で分けて近似曲線引いたほうがデータに即したもになっていそうです。 　ただ、3.5週目という境界線に関しては、 > 本書 > 3週と4週の間で急に変化していることがわかります。そこで、3.5週を堺にしてデータを分類し〜 　ということしか書かれていないので、ここは人間的な感性でやるのか、計算で求めるのかわからないところです。。 <br /><br /> #### 訓練データとテストデータ 　上記で求めたモデルの評価方法は、一般的に近似誤差などからもとめることができます。 ``` python def error(f, x, y): return sp.sum((f(x)-y)**2) f2p, residuals, rank, sv, rcond = sp.polyfit(x, y, 2, full=True) f2 = sp.poly1d(f2p) print(" error : %s" % error(f2, x, y)) # => error : 182006476.432 ``` 　しかし、これは現行のデータでの誤差の大きさを比較するための評価方法であり、未来のデータから予測することではありません。 　そこで、全データの数%だけを保持し、のこりのデータで学習を行う（*訓練データ*）。保持していたデータを用いて誤差を計算する（*テストデータ*）という手法があります。 　訓練データとテストデータを別に分けているため、「学習モデルが新しいデータについてどう振る舞うか」という現実的な視点で評価が可能となります。 <br /> <br /> 　今回取り上げているデータの中で、特に変化点以降のデータに関しての各次数の近似曲線を評価を行っていきます。 ``` python # 変化点以降（3.5週）のデータを使用して学習したデータ # テストデータ（3割）を用いた誤差を計算 frac = 0.3 split_idx = int(frac * len(xb)) shuffled = sp.random.permutation(list(range(len(xb)))) #全データの30%をランダムに選ぶ test = sorted(shuffled[:split_idx]) #テスト用のデータインデックス配列 train = sorted(shuffled[split_idx:]) #訓練用のデータインデックス配列 fbt1 = sp.poly1d(sp.polyfit(xb[train], yb[train], 1)) fbt2 = sp.poly1d(sp.polyfit(xb[train], yb[train], 2)) fbt3 = sp.poly1d(sp.polyfit(xb[train], yb[train], 3)) fbt10 = sp.poly1d(sp.polyfit(xb[train], yb[train], 10)) fbt100 = sp.poly1d(sp.polyfit(xb[train], yb[train], 100)) for f in [fbt1, fbt2, fbt3, fbt10, fbt100]: print("Error d=%i : %f" % (f.order, error(f, xb[test], yb[test]))) ``` <br /> 結果 ``` bash Error d=1 : 8021909.961602 Error d=2 : 7573035.010515 Error d=3 : 7715817.328974 Error d=10 : 9501329.363086 Error d=53 : 10333050.345188 ``` 　この結果から、次数が２のモデルの誤差が最小となりました。 　訓練データを用いて訓練する、テストデータを用いて誤差を判定するという方法では、テストデータが完全に独立しているため、未来の新しいデータに対しても信頼できるという前提となっているわけですね。 <br /><br /> #### 今回の最初の質問に対する答え 　上記で導き出したモデルを用いて、*時間あたりのリクエストが100,000を超える時期を予想する*という本来の目的に取り組んでいきます。 ``` python from scipy.optimize import fsolve reached_max = fsolve(fbt2 - 100000, 800) / (7*24) print("100,000 hits/hour expected at week %f " % reached_max[0]) ``` ``` bash 100,000 hits/hour expected at week 9.094845 ``` 　本データの最終週を4.5週目と考えると、9.1週目に100,000 hits/hourを超えるということがこのコードからわかります。 <br /> #### まとめ 　ここまでで当初目的としていた問題の解決を行いました。 　今回取り上げた解決方法で一番重要なことは、 > 本書より > 予測に関しては不確かさが伴います。さらに現状を理解するためには、より洗練された統計手法を取り入れることで、変化についてさらに深く理解し、遠い未来について予測することができます。 ということです。 ### 次回 　アイリスデータセットなどを用いて、自力で実装できる単純なアルゴリズムを用いて学ぶことにより、クラス分類について基本的な原理を理解していきます。