MachineLearning(9) OREILLY(6) Python(9)

<center> <a rel="nofollow" href="http://www.amazon.co.jp/gp/product/4873116988/ref=as_li_tf_il?ie=UTF8&camp=247&creative=1211&creativeASIN=4873116988&linkCode=as2&tag=koucs06-22"><img border="0" src="http://ws-fe.amazon-adsystem.com/widgets/q?_encoding=UTF8&ASIN=4873116988&Format=_SL250_&ID=AsinImage&MarketPlace=JP&ServiceVersion=20070822&WS=1&tag=koucs06-22" ></a><img src="http://ir-jp.amazon-adsystem.com/e/ir?t=koucs06-22&l=as2&o=9&a=4873116988" width="1" height="1" border="0" alt="" style="border:none !important; margin:0px !important;" /> </center> ### 2章 実例を対象とした分類法入門 #### ロードマップ 　[前回（第3回）まで](http://koucs.com/articles/11)の記事では以下のことを学びました。 - 機械学習の作業において基本的なデータを理解し・扱いやすい形に整形すること - 正しく評価するために*訓練データ*と*テストデータ*を分類する 　第2章からは、機械学習のためのツールキットとなる*scikit-learn*を用いて、機械学習の種類と特徴エンジニアリングについて学んでいきます。 　基本的な機械学習の活用例として、花の写真からその品種を当てることが出来るのかという問題解決があります。 　そこで、その判断のもととなる*分類方法（ルール）*を、**品種別の花のデータを用意してコンピュータに学習させていくこと**を以下のように呼びます。 - クラス分類 - 教師あり学習（supervised learning） 　本章ではこれについての概要を、アイリスデータセットというサイズの小さなデータセットから学んでいくことが目的です。 <br /><br /> #### 2.1 アイリスデータセット 　アイリスデータセットは1930年代から使われている伝統的なデータセットで、アイリスという花の一種の品種に分類するために用いられるサンプルデータより構成されています。 　近年ではDNA情報より種の選別がされていますが、1930年当時は形状により種の選別がされていたようです。 ##### 2.1.1 可視化 アイリスデータセットをグラフに描画してみます。 ``` python # coding: UTF-8 from matplotlib import pyplot as plt from sklearn.datasets import load_iris import numpy as np def apply_mode( example ): if example[best_fi] < best_t: print 'Iris Setosa' else: print 'Iris Virginics or Iris Versicolor' # Loading Data by load_iris function of sklearn data = load_iris() # features（特徴量） # [:, 0] : がく片の長さ：sepal length (cm) # [:, 1] : がく片の幅：sepal width (cm) # [:, 2] : 花弁の長さ：petal length (cm) # [:, 3] : 花弁の幅：petal width (cm) features = data['data'] feature_names = data['feature_names'] # target_names # 三角形印: Setosa（target==0） # 丸　　印: Versicolor（target==1） # バ ツ 印: Verginica（target==2） target = data['target'] target_names = data['target_names'] # targetの0,1,2の値をラベルに変換 labels = target_names[target] pairs = [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)] for i, (p0, p1) in enumerate(pairs): plt.subplot(2, 3, i + 1) for t, marker, c in zip(range(3), ">ox", "rgb"): plt.scatter(features[target == t, p0], features[ target == t, p1], marker=marker, c=c) plt.xlabel(feature_names[p0]) plt.ylabel(feature_names[p1]) plt.xticks([]) plt.yticks([]) plt.savefig('./images/ch2-1_plt1.png') ```  花の種類は - 三角形印: Setosa（target==0） - 丸印: Versicolor（target==1） - バツ印: Verginica（target==2） データの種類はpetal（花弁）、sepal（がく片）の長さ、広さです。 この画像より、*大きく２つのグループ（Verginica,VersicolorグループとSetosaグループ）に分割できそうであることがわかります。 ###### Verginica,VersicolorとSetosaの分類 　ここで、この中でVerginica,VersicolorグループとSetosaグループを分類するため、「花弁の長さ（petal lenght）」での分類を考えてみます。 　以下のコードで境界線を探してみます。 ``` python # 花弁の長さ index#2 plength = features[:, 2] is_setosa = (labels == 'setosa') # setosa かどうかのboolean配列を生成 max_setosa = plength[is_setosa].max() min_non_setosa = plength[~is_setosa].min() print('Maximum of setosa: (0) . ' + format(max_setosa)) print('Minimum of others: (0) . ' + format(min_non_setosa)) # Output # Maximum of setosa: (0) . 1.9 # Minimum of others: (0) . 3.0 ``` 　これより、Verginica,VersicolorグループとSetosaグループを分類するため、「花弁の長さ（petal lenght）」で分類出来ることがわかりました。 　人間の目でも簡単にわかる分類です、一つの次元（特徴量）において閾値を決めるだけですもんね。。。 　 ###### Verginica　と　Versicolor　の分類 　上の画像で見た限りでもわかるように、VerginicaとVersicolorは綺麗に分割することはできないように思えます。 　そこで単純な方法から分類を行ってみます。 ``` python from matplotlib import pyplot as plt from sklearn.datasets import load_iris import numpy as np def apply_mode( example ): if example[best_fi] < best_t: print 'Iris Setosa' else: print 'Iris Virginics or Iris Versicolor' # Loading Data by load_iris function of sklearn data = load_iris() # features（特徴量） # [:, 0] : がく片の長さ：sepal length (cm) # [:, 1] : がく片の幅：sepal width (cm) # [:, 2] : 花弁の長さ：petal length (cm) # [:, 3] : 花弁の幅：petal width (cm) features = data['data'] feature_names = data['feature_names'] # target_names # 三角形印: Setosa（target==0） # 丸　　印: Versicolor（target==1） # バ ツ 印: Verginica（target==2） target = data['target'] target_names = data['target_names'] # targetの0,1,2の値をラベルに変換 labels = target_names[target] is_setosa = (labels == 'setosa') # setosa かどうかのboolean配列を生成 features = features[-is_setosa] labels = labels[-is_setosa] virginica = (labels == 'virginica') best_acc = -1.0 best_fi = -1.0 best_t = -1.0 count_virginica = float(list(labels == 'virginica').count(True)) for fi in xrange(features.shape[1]) : # 各特徴量ごとにしきい値の候補を生成 thresh = features[:, fi].copy() thresh.sort() # 全ての閾値でテスト for t in thresh: pred = (features[:, fi] > t) # ある閾値（t）以上のリストの中に含まれているveriginicaの数と # 全体のverginicaの数（count_verginica） # の比 acc1 = list(labels[pred] == 'virginica').count(True) / count_virginica # ある閾値（t）以上のリストの中に含まれているveriginicaの数 # ある閾値（t）以上のリストに含まれている閾値以上の要素の数 # の比 if float(list(pred).count(True)) != 0.0: acc2 = list(labels[pred] == 'virginica').count(True) / float(list(pred).count(True)) # print('['+format(t)+']'+' acc1 : '+format(acc1)+', acc2: '+format(acc2)) if acc2 != 0.0 : acc = acc1*acc2 if acc > best_acc: best_acc = acc best_fi = fi best_t = t # print ('fi = '+format(fi)+', best_acc = '+format(best_acc)+', best_fi='+format(best_fi)+', best_t='+format(best_t)) print('best_acc : '+format(best_acc)) print('best_fi : '+format(best_fi)) print('best_t : '+format(best_t)) ``` ``` python is_setosa = (labels == 'setosa') # setosa かどうかのboolean配列を生成 features = features[-is_setosa] labels = labels[-is_setosa] virginica = (labels == 'virginica') ``` ここではis_setosaを用いてSetosa以外の2品種の配列を作成しています。 それ以降は長々と書いていますが、簡潔には以下の流れで最適な境界線を決定しています。 1. 2品種のデータそれぞれのデータを```thresh```に格納 2. threshを昇順にsort 3. threshの各値を境界線とした際の、acc1とacc2を計算 - acc1 : 閾値（t）以上のリストの中に含まれているveriginicaの数 / 全体のverginicaの数 - acc2 : 閾値（t）以上のリストの中に含まれているveriginicaの数 / ある閾値（t）以上のリストに含まれている閾値以上の要素の数 - これは、閾値自体の正確さを、閾値以上に含まれるデータの数と閾値に含まれるべき正解の数の２つの側面から正確性（accuracy）を計算し、掛けあわせたものである。 **※ このaccの計算方法は、著書の付属コードから自分で少しカスタマイズしています。** この決定された境界線を持ちいて分類してみると、おおよそ以下の様な分類ができます。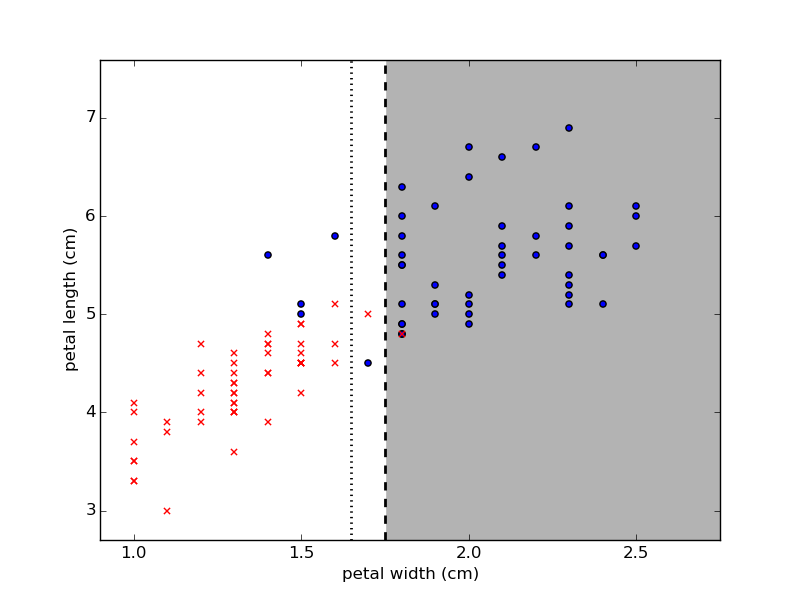  ###### 交差検定（cross-validation） 上記の境界線を評価する上では、best_accなどで計算をしていましたが、これでは 　*訓練データから導いた境界線を訓練データで評価すること* となり、今回のような単純なデータならともかく、複雑なモデルであれば有るほど、新規データに対する信頼性が低くなることが予想されます。 　 全てのデータを訓練・テストに用いることが理想的ですが、それに近いことを行うのが*交差検定*です。 文章で説明するより、以下の画像がわかりやすいでしょう。 >  > > モデルの精度を推定する > http://musashi.osdn.jp/tutorial/mining/xtclassify/accuracy.html 実際に用いられるテストサイズは、全体の1/5、つまり20%のでーたを訓練用として用いるということが一般的なようです。（分割数が5だと5-分割交差検定） #### 2.1 まとめ 　ここでは、アイリスデータセットを用いて簡単な境界線の決定、その境界線の評価を交差検定で行うことを学びました。 　僕個人としては、境界線云々よりも*交差検定*のことのほうが重要であると思えるので、ここをもっと深掘りしても良いのかと思いました。